DYNAMO is the main mechanism for the generation and maintenance of magnetic fields in stars, planets and exo-planetes. Observations (Donati et al., ARAA,
2009), experiments and simulations [125] reveal that rotation is one of the key factors that determines the main characteristics of the observed magnetic fields
like its strength or its structure (e.g. dipolar or multipolar, erratic or time-periodic). Observations show that fast
rotating stars tend to have strong dipolar fields while weakly rotating stars have multipolar fields of weaker strength. Several dynamo experiments
(with liquid metals) have been/are being built for which rotation is an integral part of the experimental set-up, and can play crucial role since it
controls the complexity of the resulting flow (see e.g. Berhanu et al., Europhys. Lett., 2007).
Rotation affects a turbulent flow in two ways. Fast rotation renders the flow quasi two-dimensional, and at the same time inertial waves that exist in
the presence of rotation alter the cascade of energy towards small scales making the cascade weaker [26,98] and modifying the energy spectrum down to scales
where the rotation rate is larger than vorticity. Although rotation plays an important role in the dynamo process, a qualitative description of the possible
dynamo regimes is still lacking. The fluid description used to investigate the dynamo mechanism is MHD [105]. In this framework, I derived a wave turbulence theory
for fast rotating MHD [99]. The theory gives some answers about the statistical behaviour of such a flow subject to a forcing at intermediate scales and in
which Alfvén, inertial and magnetostrophic waves are present. For example, an inverse cascade of hybrid helicity (a combination of magnetic helicity
and cross-helicity) is predicted at scales larger than the forcing scale only when the rotating axis is parallel to the large-scale magnetic field.
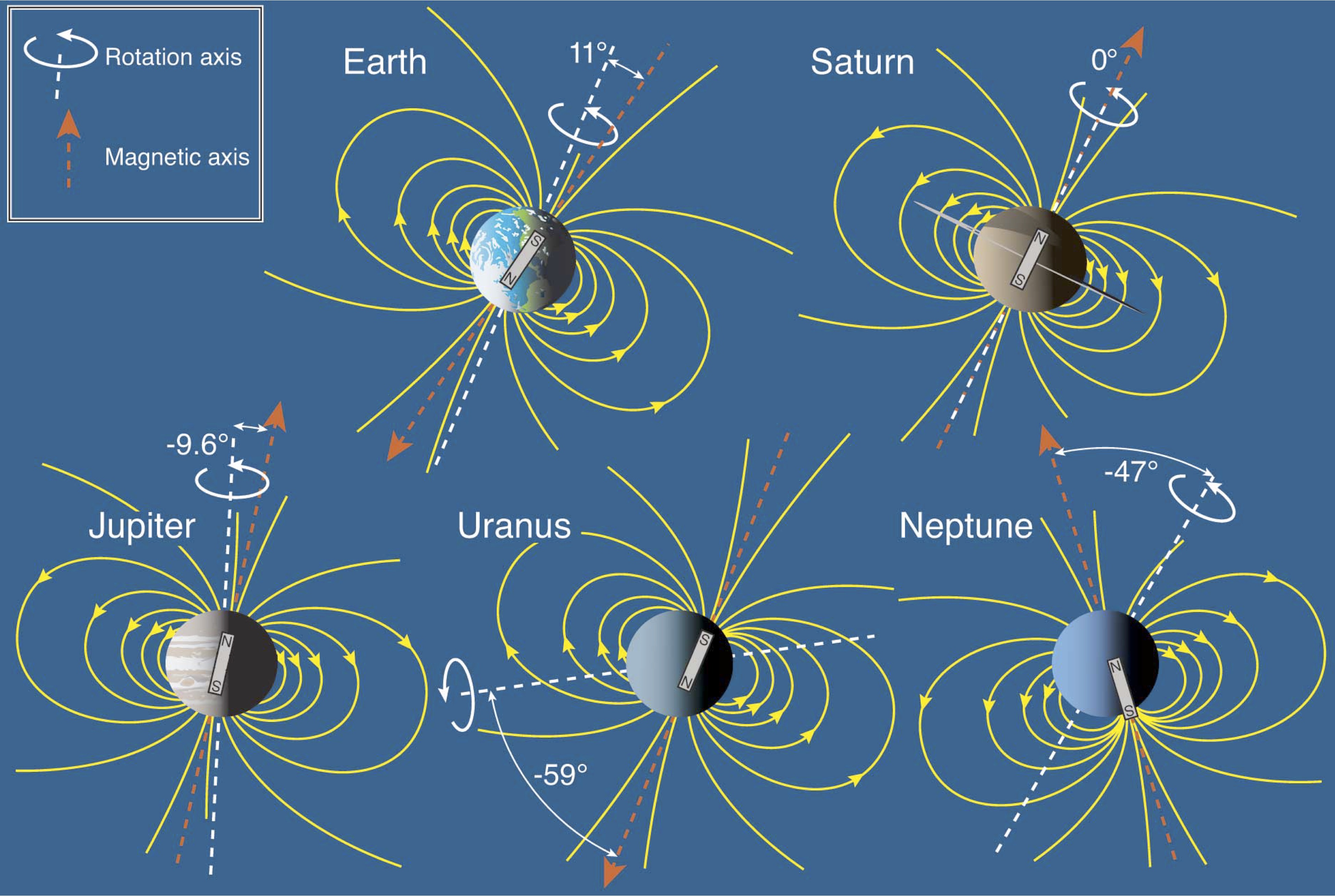
In other words, the maintenance of a magnetic field seems only possible in this configuration. It is precisely the situation observed for planets like Earth,
Jupiter or Saturn. In this context, we have recently studied the regime of strong magnetostrophic wave turbulence with direct numerical simulations. We have confirmed that
the inverse cascade of hybrid helicity is magnified when the rotation rate is aligned with the uniform
magnetic field [120]. Interestingly, the regime of magnetostrophic wave turbulence shares many properties with whistler wave turbulence [30] that is evoked to explain
sub-ionic solar wind turbulence. This similitude may help to investigate numerically rotating dynamos since several papers devoted to electron MHD turbulence –
with its generalization to Hall MHD – have been published [88,96,116,121].